Lie Group

Lie Group 李群
同时具有群结构和流形结构的数学对象

Lie群是一种可以平滑变化的连续群，群元素之间不仅可以做代数运算，而且可以连续移动、微分、优化。

一个集合 $G$ 是一个 Lie 群，当且仅当满足以下两个条件：

$G$ 是一个群，群运算 $\cdot : G \times G \to G$ 和取逆运算 $inv : G \to G$ 满足：
- 封闭性：对于所有 $a, b \in G$ ，有 $a \cdot b \in G$ 。
- 结合性：对于所有 $a, b, c \in G$ ，有 $(a \cdot b) \cdot c = a \cdot (b \cdot c)$ 。
- 单位元存在：存在元素 $e \in G$ ，使得对于所有 $a \in G$ ，有 $e \cdot a = a \cdot e = a$ 。
- 逆元存在：对于所有 $a \in G$ ，存在 $a^{- 1} \in G$ ，使得 $a \cdot a^{- 1} = a^{- 1} \cdot a = e$ 。
$G$ 是一个光滑流形，且群运算和取逆运算是光滑（可微）映射：
- $μ : G \times G \to G, μ (a, b) = a \cdot b$
- $ι : G \to G, ι (a) = a^{- 1}$

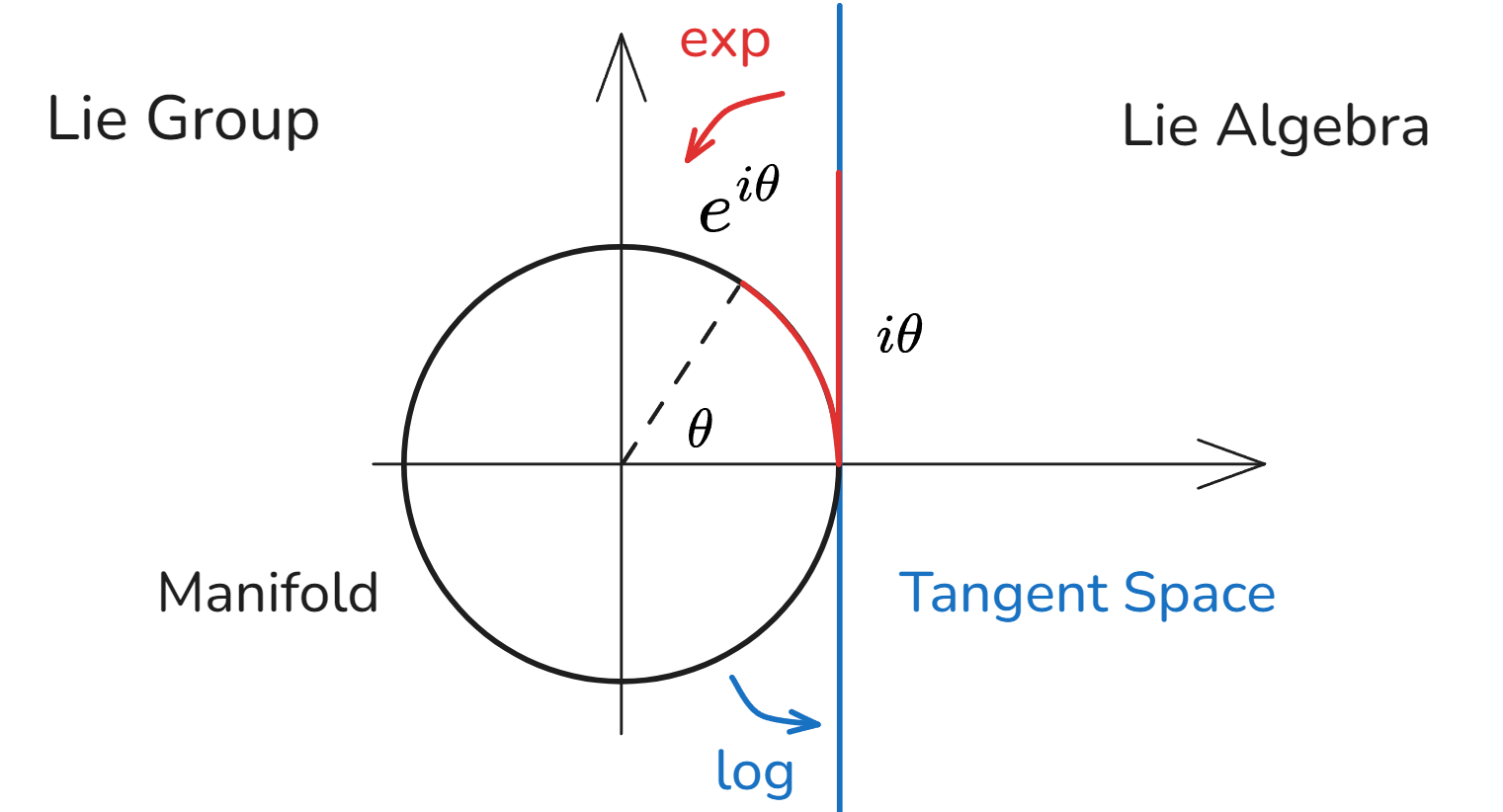
Lie群的微分结构由其李代数（Lie Algebra）描述。
Lie Group 描述全局运动（非线性），Lie Algebra 描述局部运动（线性）。

Lie 群	群元素形式	Lie 代数	解释	在机器人中的应用
$S O (2)$	$2 \times 2$ 旋转矩阵	$ω \in R$	二维平面旋转群	平面机器人、移动机器人姿态
$S O (3)$	$3 \times 3$ 旋转矩阵	$ω \in R^{3}$	三维空间旋转群	三维姿态，机械臂关节、无人机
$S E (2)$	$3 \times 3$ 刚体变换矩阵	$[v, ω] \in R^{3}$	平面刚体运动群（位置+角度）	移动机器人位姿
$S E (3)$	$4 \times 4$ 刚体变换矩阵	$[v, ω] \in R^{6}$	空间刚体运动群（位置+姿态）	机械臂末端运动、无人机运动
$R^{n}$	向量加法	向量本身	欧式空间，平移群	位置变化

应用	说明
机械臂运动学	末端轨迹在SE(3)空间规划
位姿估计	视觉 SLAM、IMU 积分，利用SO(3)、SE(3)误差模型
轨迹学习	PRIMP 等方法在SE(3)上建模轨迹概率分布
运动规划	Workspace-STOMP等算法在Lie 群上定义代价函数
视觉变换	相机坐标系转换